
廢話不多說,鬼故事馬上開始。
司馬億每天上班的通勤時間,大約為65分鐘。
時間確實長了些,但再忍忍也就過去了。
畢竟新修的道路不日將開放,自己再也不用起得比雞還早啦。

然而,恐怖的事情就發生在這條新路開通的那天。
兢兢業業的司馬億,高高興興地出門——卻破天荒地遲到了。
路程明明比平時短得多,但花的時間竟比平時還多了整整15分鐘。
司馬億這個月的全勤獎,也隨之化為泡影。

事實上,這種詭異的情況在現實中還真不少見。
明明增加了路線,但堵車的情況卻更加嚴重了。
而這種吃力不討好且反常識的交通網絡現象,便是著名的布雷斯悖論,由德國數學家迪特里希·布雷斯(Dietrich Braess)於1968年提出。

1977年的布雷斯
在這個悖論面前,我們常識中的「多修路能化堵」,仿佛也失效了。
當在一個繁忙的交通網上,新增加一條線路。
這條新增的線路不但沒有辦法減輕交通的延滯,反而還會拉低整個交通網絡的服務水準。
如果覺得不可思議,不妨看一下這個概念模型。
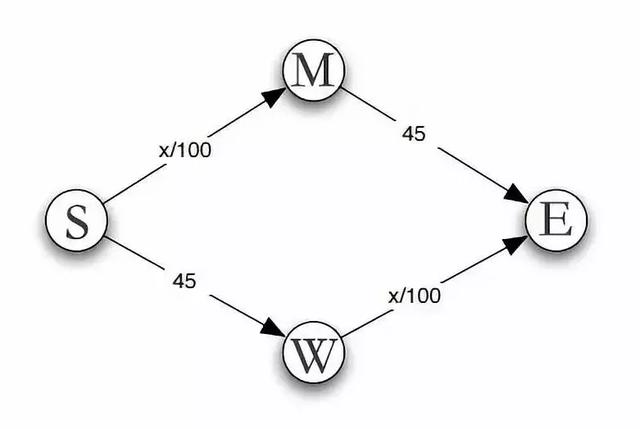
每天都有一批人必須從S點前往E點。
而想要完成這段路程,共有2條線路,分別為SME或SWE。
其中SW與ME的路況較好,無論有多少車輛駛過都只需要45分鐘。
但SM段與WE段就不同了,比較容易堵車:隨著車流量x的增大,所需時長(x/100)也會增加。

現在假設每天都會有4000輛小汽車會從起點S前往終點E。
這時,一場博弈已經展開了,站在分叉路口上的老司機會選擇走哪條路呢?
如果有a人選擇走SME路線,那麼總時長則為a/100+45,而走另一條路SWE的總時長則為45+(4000-a)/100。
由此可見,無論哪條路人更多,該路段的通行時間就會越長。

當然,司機們一開始也無法得知其他人會如何選擇路線,便會偏向於隨機選擇一邊。
司馬億每天上班,也同樣要經歷這樣的抉擇。
但到後來,如果SME所花時間多,大家便會湧向SWE。
而SWE的人多了所花時間變長了,人們又會自然回到SME。
最終,這兩條路都會平均分攤到2000輛的車流量,通行時間固定為2000/100+45=65分鐘。
以上,便是修路之前的大致狀況了。現在我們就來修路吧,看看會發生什麼?
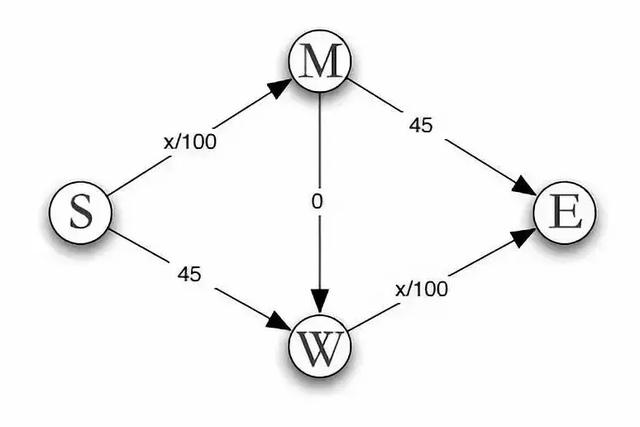
如圖所示,在MW之間新增一條快速通道,使得M與W連成一體。
這條路暢通得「如飛一般的感覺」,所花時間幾乎可以忽略不計,設為0。
這對全體司機來說,無疑是件大好事。
而且說MW路段是捷徑都不為過,他們每一個人都能從這段新路中獲得優勢。

在這種情況下,就算SM與WE路段擠滿了人(即x=4000),這兩段路的耗時也只需4000/100=40分鐘。
所以相比另外兩段路(SW與ME)固定耗時45分鐘,走SM與WE路段始終耗時更短。
而我們也注意到,此刻原來兩條路線SME與SWE均需要花費85分鐘。

經濟學中假設每個司機都是自私自利的,他們必然會選擇對自己最有益的路線。
於是,所有人會毫不猶豫地選擇SMWE這條新路。
用80分鐘(4000/100+0+4000/100=80)走完全程。
但是回過頭看看才發現,大家都被坑了。
原本在不修這條該死的新路前,無論走哪條路都只需要65分鐘。
驚不驚喜,意不意外,多修了一條近路,司機的總通行時長反而增加了。
所以,這也是司馬億為什麼遲到的原因,一目了然。

我們可以注意到,正是「自私」造成了這種困境。
事實上,如果所有司機約定好犧牲一下走回原來的老路,大家都會比現狀好些,至少每人都能節省個15分鐘。
但在利益面前,人都是趨利的,這也是布雷斯悖論的關鍵所在。
在這個4000人的博弈中,你個人的選擇已經不太重要了,其他的3999人才是重點。

於是我們可以看到,大家都競相選擇最有利的路線。
最後卻在無形中之中,使得交通系統崩潰。
這也是納什均衡中提到的,個體聰明選擇的匯總,其實並非最優解。
所以加入了新的道路,反而讓所有人都陷入了「囚徒困境」式的納什均衡。
而大家都因忌諱損害自身的利益而選擇抄近路,則是布雷斯悖論中的納什均衡點。
身陷這個龐大的漩渦,司馬億遲到都是可以預料的後果了。

斯圖加特風光
在現實生活,這種好心辦壞事的例子可不少見。
例如,1969年德國的斯圖加特市添加了一條新道路,就是為了解決交通不順暢的老毛病。
沒想到卻得了反效果,交通狀況更是惡化,堵得水泄不通。
絕望的政府只好把這些路段去掉,交通才得以恢復原狀。
所以反過來,許多大城市也曾參考這個理論來制定了政策。
有時只需把「多餘」的路封掉,就能提高道路網絡的整體效率。
